TEORIA DE CONJUNTOS

Conjunto Disjunto, Conjunto Subconjunto
1) Conjuntos disjuntos: Son aquellos conjuntos que no tienen elementos en común.
Por ejemplo:              
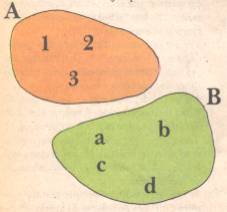
El conjunto A tiene como elementos a los números 1, 2 y 3. El conjunto B tiene como elementos a las letras a, b, c y d. No hay elementos comunes entre los conjuntos A y B. En otras palabras, ningún elemento del conjunto A pertenece al conjunto B; a su vez, ningún elemento de B pertenece al conjunto A.
En consecuencia, los conjuntos A y B son disjuntos.


Tomando otro ejemplo:
Si  E = { pizarrón, tiza, borrador} (Conjunto E formado por pizarrón, tiza, borrador)
     F =  { tiza, profesor, regla}   (Conjunto F formado por tiza, profesor, regla)
G = { niño, cuaderno, sala, lápiz } (Conjunto G formado por niño, cuaderno, sala, lápiz)
E y G son conjuntos disjuntos porque: pizarrón, tiza, borrador no pertenecen al conjunto G.  
E y F no son disjuntos ya que  tiza pertenece a  E y también a  F.
F y G son conjuntos disjuntos porque: tiza, profesor, regla no pertenecen a G, y niño, cuaderno, sala, lápiz no pertenecen a F.
2) Conjunto Subconjunto: Un conjunto es subconjunto de otro si todos los elementos de un conjunto también pertenecen al otro.
Si se tienen los siguientes conjuntos:

P = { a, e, i, o, u }                 y                    R = { a, i } 

R es subconjunto de P porque todos los elementos de R están en P.
En general, para expresar que un conjunto es subconjunto de otro conjunto se pone entre ellos el símbolo  . En este ejemplo se escribe:

R   P

Se lee “ R es subconjunto de P”
no es subconjunto de otro cuando al menos un elemento del primero no pertenece al segundo conjunto. El símbolo que representa la frase “no es subconjunto de“ es .
Si se tienen los siguientes conjuntos:

C =  { 3, 5, 7, 9 }                 y                   H =  { 3, 5, 8  }

H no es subconjunto de C porque el elemento 8 no pertenece al conjunto C. Se escribe:

H   C

Se lee “ H no es subconjunto de C”
También los subconjuntos pueden representarse mediante Diagramas de Venn.
Ejemplo:
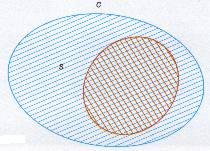                                 S      C

Propiedades de la relación subconjunto
1.- Todo conjunto es subconjunto de sí mismo.
                    Si   T =  { x, z, y, z  }, se tiene que  T  T
2.- El conjunto vacío es subconjunto de cualquier conjunto (el conjunto vacío es aquel que no tiene elementos; se representa por: { } o bien por Ø
Si se tiene el conjunto B se puede establecer que   Ø    T